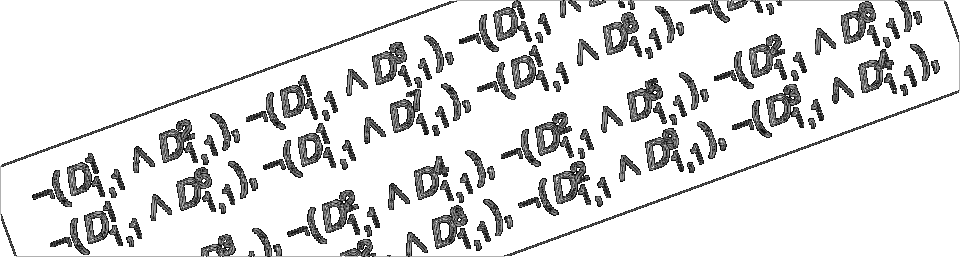The KeY System is a formal software development tool that aims to integrate design, implementation, formal specification, and formal verification of object-oriented software as seamlessly as possible. At the core of the system is a novel theorem prover for the first-order Dynamic Logic for Java with a user-friendly graphical interface.
The project was started in November 1998 at the University of Karlsruhe. It is now a joint project of KIT, Chalmers University of Technology, Gothenburg, and TU Darmstadt. The KeY tool is available for download